Linear Regression: First Step into Machine Learning
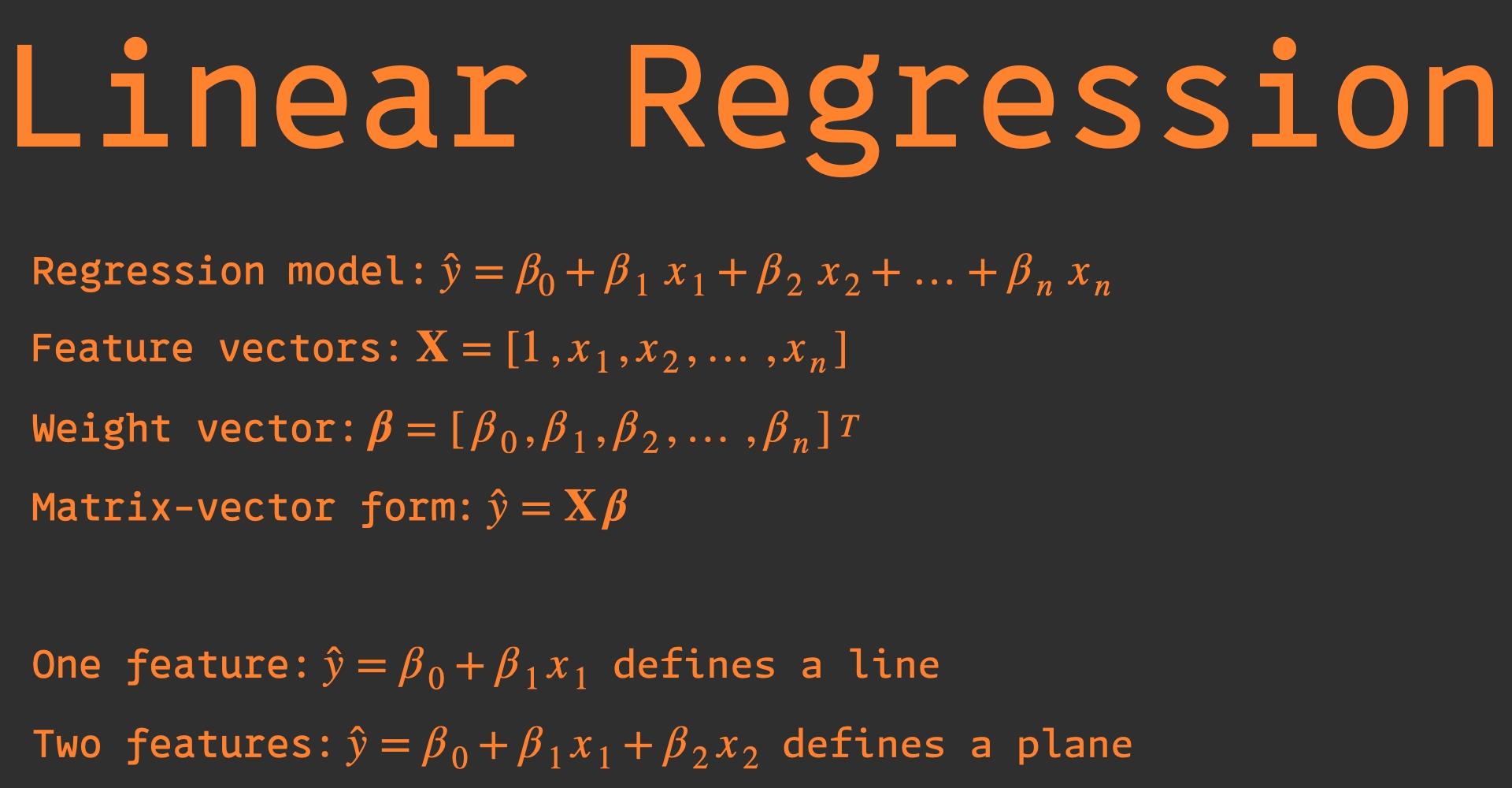
Linear regression is one of the most fundamental techniques in machine learning and statistics. It models the relationship between a continuous target variable and one or more input features by fitting a straight line (or hyperplane) through the data.
The core idea is simple: given data points, find the line that best describes the relationship between variables. Once you have this line, you can use it to predict new values.
Linear regression is useful because it’s:
- Easy to understand and implement
- Fast to train and make predictions
- Provides interpretable results
- Works well as a baseline model
This article covers the basics of linear regression, from simple to multiple regression, with Python implementations and practical considerations.
What is Linear Regression?#
Linear regression assumes there’s a linear relationship between input variables (features) and the output variable (target). The goal is to find the best line that fits through the data points.
The Math#
The basic equation is:
\[ y = \beta_0 + \beta_1\, x + \epsilon \]Where:
- \( y \) is what you want to predict (target)
- \( x \) is your input feature
- \( \beta_0 \) is the y-intercept
- \( \beta_1 \) is the slope
- \( \epsilon \) is the error term
How It Works#
- Take your training data (\( x \), \( y \) pairs)
- Find the line that minimizes the distance between actual and predicted values
- Use this line to predict new values
Types#
- Simple linear regression: One input feature (\( x \) predicts \( y \))
- Multiple linear regression: Multiple input features (\( x_1 \) , \( x_2 \) , \( x_3 \) … predict \( y \))
The algorithm learns the best values for \( \beta_0 \) and \( \beta_1 \) (or multiple \( \beta \) values in multiple regression) by minimizing prediction errors.
Simple Linear Regression with Python#
Simple linear regression uses one feature to predict a target. Let’s implement it from scratch and then use scikit-learn.
The Method: Ordinary Least Squares (OLS)#
OLS finds the line that minimizes the sum of squared errors between actual and predicted values. It’s the most common approach because:
- Simple to compute
- Has a closed-form solution
- Gives interpretable results
Python Implementation#
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# Sample data: house size vs price
size = np.array([1000, 1500, 2000, 2500, 3000]).reshape(-1, 1)
price = np.array([200000, 300000, 400000, 500000, 600000])
# Create and train model
model = LinearRegression()
model.fit(size, price)
# Get predictions
predictions = model.predict(size)
# Model parameters
print(f"Intercept (β₀): {model.intercept_}")
print(f"Slope (β₁): {model.coef_[0]}")
print(f"MSE: {mean_squared_error(price, predictions)}")
# Make a prediction
new_size = np.array([[2200]])
predicted_price = model.predict(new_size)
print(f"Predicted price for 2200 sq ft: ${predicted_price[0]:,.0f}")
Key Points#
- MSE (Mean Squared Error): Measures how well the line fits. Lower is better.
- Outliers matter: One extreme value can shift the entire line significantly.
- Linear assumption: Only works well when the relationship is actually linear.
Multiple Linear Regression with Python#
Multiple linear regression uses several features to predict a target. The equation becomes:
\[ y = \beta_0 + \beta_1\, x_1 + \beta_2\, x_2 + \ldots + \beta_n\, x_n + \epsilon \]Python Implementation#
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# Sample data: house features vs price
data = pd.DataFrame({
'size': [1000, 1500, 2000, 2500, 3000, 1200, 1800, 2200],
'bedrooms': [2, 3, 4, 4, 5, 2, 3, 4],
'age': [10, 5, 1, 8, 15, 12, 3, 6],
'price': [200000, 300000, 400000, 480000, 550000, 220000, 350000, 420000]
})
# Features and target
X = data[['size', 'bedrooms', 'age']]
y = data['price']
# Create and train model
model = LinearRegression()
model.fit(X, y)
# Get predictions
predictions = model.predict(X)
# Model parameters
print(f"Intercept (β₀): {model.intercept_:,.0f}")
print("Coefficients:")
for feature, coef in zip(X.columns, model.coef_):
print(f" {feature}: {coef:,.2f}")
print(f"R² Score: {r2_score(y, predictions):.3f}")
print(f"MSE: {mean_squared_error(y, predictions):,.0f}")
# Make a prediction
new_house = pd.DataFrame({
'size': [2100],
'bedrooms': [3],
'age': [5]
})
predicted_price = model.predict(new_house)
print(f"Predicted price: ${predicted_price[0]:,.0f}")
Key Considerations#
- Multicollinearity: When features are highly correlated, coefficients become unstable
- Feature scaling: May be needed when features have very different ranges
- More features ≠ better: Risk of overfitting increases with more variables
- R² score: Shows proportion of variance explained by the model (closer to 1 is better)
Evaluating Your Model#
After training a linear regression model, you need to assess how well it performs. Here are the key metrics and how to implement them.
Common Metrics#
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
# Assuming we have actual and predicted values
y_actual = np.array([200000, 300000, 400000, 500000, 600000])
y_predicted = np.array([190000, 310000, 395000, 520000, 580000])
# Mean Squared Error (MSE)
mse = mean_squared_error(y_actual, y_predicted)
print(f"MSE: {mse:,.0f}")
# Root Mean Squared Error (RMSE)
rmse = np.sqrt(mse)
print(f"RMSE: {rmse:,.0f}")
# Mean Absolute Error (MAE)
mae = mean_absolute_error(y_actual, y_predicted)
print(f"MAE: {mae:,.0f}")
# R² Score (Coefficient of Determination)
r2 = r2_score(y_actual, y_predicted)
print(f"R² Score: {r2:.3f}")
What These Metrics Mean#
- MSE: Average squared difference between actual and predicted values. Lower is better.
- RMSE: Square root of MSE. Same units as your target variable. Easier to interpret.
- MAE: Average absolute difference. Less sensitive to outliers than MSE.
- R²: Proportion of variance explained by the model. 1.0 = perfect fit, 0.0 = no better than guessing the mean.
Residual Analysis#
# Calculate residuals
residuals = y_actual - y_predicted
# Plot residuals
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.scatter(y_predicted, residuals)
plt.axhline(y=0, color='red', linestyle='--')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residuals vs Predicted')
plt.subplot(1, 2, 2)
plt.hist(residuals, bins=10)
plt.xlabel('Residuals')
plt.ylabel('Frequency')
plt.title('Residual Distribution')
plt.tight_layout()
plt.show()
What to Look For#
- Random residuals: Good - means the model captured the pattern
- Patterns in residuals: Bad - suggests missing non-linear relationships
- Normal distribution of residuals: Good - validates model assumptions
Common Pitfalls and How to Avoid Them#
1. Outliers Skewing Results#
Problem: One extreme data point can drastically shift your regression line.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Data with an outlier
X = np.array([1, 2, 3, 4, 5, 100]).reshape(-1, 1)
y = np.array([2, 4, 6, 8, 10, 15])
model = LinearRegression()
model.fit(X, y)
print(f"Slope with outlier: {model.coef_[0]:.3f}")
# Remove outlier and refit
X_clean = X[:-1]
y_clean = y[:-1]
model_clean = LinearRegression()
model_clean.fit(X_clean, y_clean)
print(f"Slope without outlier: {model_clean.coef_[0]:.3f}")
Solution: Examine your data, identify outliers using plots or statistical methods, decide if they’re errors or valid extreme cases.
2. Assuming Linear Relationships#
Problem: Forcing a straight line through curved data gives poor predictions.
# Check for non-linearity
plt.scatter(X, y)
plt.plot(X, model.predict(X), color='red')
plt.title('Check if relationship looks linear')
plt.show()
Solution: Plot your data first. If it’s curved, consider polynomial features or other regression methods.
3. Multicollinearity#
Problem: When features are highly correlated, coefficients become unstable.
import pandas as pd
# Check correlation between features
df = pd.DataFrame({
'feature1': [1, 2, 3, 4, 5],
'feature2': [2, 4, 6, 8, 10], # Perfectly correlated with feature1
'target': [10, 20, 30, 40, 50]
})
correlation_matrix = df.corr()
print(correlation_matrix)
Solution: Remove highly correlated features (correlation > 0.8) or use regularization techniques.
4. Not Splitting Your Data#
Problem: Testing on training data gives overly optimistic results.
from sklearn.model_selection import train_test_split
# Always split your data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Train on training set
model.fit(X_train, y_train)
# Evaluate on test set
test_predictions = model.predict(X_test)
train_predictions = model.predict(X_train)
print(f"Train R²: {r2_score(y_train, train_predictions):.3f}")
print(f"Test R²: {r2_score(y_test, test_predictions):.3f}")
Solution: Always reserve some data for testing that the model never sees during training.
5. Ignoring Feature Scaling#
Problem: Features with large values dominate those with small values.
from sklearn.preprocessing import StandardScaler
# Example: age (0-100) vs income (0-100000)
# Scale features to have similar ranges
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
Solution: Scale features when they have very different ranges, especially for regularized regression.
When to Use Linear Regression#
Good Use Cases#
Use linear regression when:
- The relationship between features and target appears linear
- You need an interpretable model (coefficients show feature importance)
- You want a fast, simple baseline model
- You have limited data (works well with small datasets)
- You need to explain your model to non-technical stakeholders
# Quick check: does your data look linear?
import matplotlib.pyplot as plt
plt.scatter(X, y)
plt.xlabel('Feature')
plt.ylabel('Target')
plt.title('Does this look like a straight line could fit?')
plt.show()
Examples Where It Works Well#
- Predicting house prices based on size, location, age
- Sales forecasting from advertising spend
- Medical dosage calculations
- Economic modeling (GDP vs other indicators)
- Simple time series with clear trends
When NOT to Use Linear Regression#
Avoid linear regression when:
- Your data has clear non-linear patterns
- You have many irrelevant features (use regularized methods instead)
- Your target variable is categorical (use classification instead)
- You need maximum predictive accuracy regardless of interpretability
# Signs you might need something else:
# 1. Residual plots show patterns (not random scatter)
residuals = y_actual - y_predicted
plt.scatter(y_predicted, residuals)
plt.axhline(y=0, color='red', linestyle='--')
plt.title('Random scatter = good, patterns = bad')
# 2. Very low R² score
r2 = r2_score(y_actual, y_predicted)
if r2 < 0.3:
print("Low R² - consider other methods")
Quick Decision Framework#
- Plot your data - does it look roughly linear?
- Check your R² - above 0.5 is usually decent for linear regression
- Look at residuals - should be randomly scattered
- Consider your goal - need interpretability or maximum accuracy?
If linear regression doesn’t work well, consider:
- Polynomial regression (for curved relationships)
- Random Forest (for complex patterns, still interpretable)
- Regularized regression (Ridge/Lasso for many features)
Next Steps#
Once you’re comfortable with linear regression, here are logical next steps to expand your regression toolkit:
Immediate Extensions#
Polynomial Regression: Handle curved relationships by adding polynomial features
from sklearn.preprocessing import PolynomialFeatures
# Transform features to include x², x³, etc.
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
Regularized Regression: Handle many features and prevent overfitting
from sklearn.linear_model import Ridge, Lasso
# Ridge regression (L2 regularization)
ridge = Ridge(alpha=1.0)
ridge.fit(X, y)
# Lasso regression (L1 regularization, does feature selection)
lasso = Lasso(alpha=1.0)
lasso.fit(X, y)
More Advanced Methods#
Tree-Based Models: Handle non-linear patterns naturally
- Random Forest: Good balance of accuracy and interpretability
- XGBoost: Often wins competitions, harder to interpret
Support Vector Regression: Good for complex patterns with the right kernel
Neural Networks: For highly complex, non-linear relationships
Key Concepts to Learn Next#
- Cross-validation for better model evaluation
- Feature engineering and selection
- Handling categorical variables
- Time series regression
- Model ensemble techniques
Practice Recommendations#
- Start with real datasets: Kaggle, UCI ML Repository
- Always begin with linear regression as your baseline
- Focus on the process: data cleaning → modeling → evaluation → interpretation
- Compare methods: see when simple linear regression is enough vs when you need more complexity
Linear regression gives you the foundation to understand all other regression methods. Master it first, then gradually add complexity only when needed.